Super-geek!

Look what arrived today!! :¬) This is yet another amazing book for the incredibly niche market that fits me so perfectly. It contains ten academic papers along with the crafting projects. Each chapter contains definitions, experiments and conjectures,  observations, theorems and corollaries, as well as advanced questions and teaching ideas for use with my students. I have the best end of term activities!! So, mostly to indulge the mathematical me, I’m going to briefly run you through the projects and principles.

1. Quilted Mobius Band

This chapter includes work on the Euler characteristic, homology groups, matrices, graph theory and map-colouring problems. The crafting item seems to be of little practical use but this particular topological structure will always hold a special significance to me. David proposed by writing the all important words on a Mobius strip and placing it in a bouquet of flowers for my 26th birthday.

2. Picking up stitches and diophantine equations

Other than the diophantine equations this paper uses algorithms and mathematical modelling as well as considering the existence and uniqueness of solutions to produce bi-directional knitted hats that do not require ‘finishing off’ at the end of the knitting process.

3. The Sierpinski variations: self-similar crochet

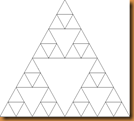The Sierpinski triangle is a fractal consisting of mathematically similar triangles produced using a simple iteration. I’ve taught lessons on ratio and proportion based on the Sierpinski triangle. It also discusses Pascal’s triangle, binomial coefficients and modular arithmetic. It contains a couple of ideas for creating crocheted shawls.

4. Only two knit stitches can create a torus

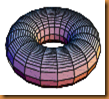Combinatorial analysis and curvature are the main discussion points in this chapter. However, they also consider a number of interesting questions such as, “How could the plain torus pattern be altered to change the ratio of the longitudinal and meridianal cycles?”

5. Symmetry patterns in cross-stitch

Whilst creating beautiful stitched patterns using the expected symmetries and transformations, the authors discuss Isometries of the Euclidean plane, group theory and how to use cross-stitch to see that tan(60o) is irrational. I love the two large patterns provided and will definitely make them at some point.

6. Socks with algebraic structure

As yet I have not mastered the art of knitting so it may be some time before I have the ability to tackle algebraic socks but I certainly can appreciate the modular arithmetic involved!

7. Fortunatus’s Purse

There is more fun to be had with topological manipulation in this chapter. The Klein bottle makes an appearance and we must consider colour theorems in the Euclidean plane and antipodal points on shapes such as dodecahedrons and truncated icosahedrons.

8. Knot cables and braids

Again, there are lots of patterns and ideas about knitting braids and cables. In the Teaching Ideas section they suggested that the braid group can provide useful examples that explore algebraic properties such as commutative and associative laws.

9. The Graph Theory of Blackwork embroidery

Eulerian graphs, Holbeinian graphs, multigraphs, Aragonian graphs, four definitions, four theorems and five corollaries, need I say more?! This chapter is a Mathematicians dream and I can’t wait to try this new craft. The final pieces are stunning.

10. Stop those pants!

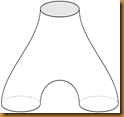Ever fancied knitting hyperbolic trousers? Well, now’s your chance. In this chapter the authors discuss the curvature of wearable trousers and how to model both constant positive and constant negative curvature from plastic.

Amazing, an inspirational, thought-provoking book that pushes all of my buttons. The next purchase will be Crocheting Adventures with Hyperbolic Planes but I guess I’d better get on and learn how to crochet first…