Although there is a second edition of this book out at the end of this month (click here for details) I only just got this one for Christmas. It’s brilliant. Mind you, it is very definitely another one of those books that will appeal to the few of us who really are passionate about both Mathematics and crafting.
This book consists of 22 activities to inspire mathematical discovery in the classroom through origami. They range from “folding equilateral triangles in a square” to “rigid folds – Gaussian curvature and spherical trigonometry”. The worksheets and solutions are carefully produced and, at least at first glance, appear to be very useable while the pedagogy and extension sections are really interesting.
Although the material is primarily aimed at higher education Mathematics courses such as topology, number theory, calculus and graph theory, many of the activities can be adapted to suit high school Mathematics too. It will just take a bit of creativity, flexibility and plenty of enthusiasm to see them through.
Once they have constructed the net of a truncated icosahedron (football), I have often challenged my key stage 4 classes to colour the net so that no two faces of the same colour touch before cutting and folding the net into the 3-dimensional shape. This book has given me some further ideas on this topic and next week I’m going to attempt to introduce my Year 10s to the concept of planar graphs allowing them to demonstrate that four colours are sufficient to colour the ball without like-coloured faces touching.
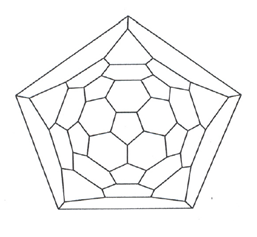
Imagine putting a football (which is made up of 20 hexagons and 17 pentagons) onto the table, stretching the bottom face out and pushing the rest of the ball down flat onto the table so that none of the edges cross. This creates the following planar graph of a truncated icosahedron:
Note that this representation only shows 31 faces as the 32nd shape (the final pentagon) is stretched out underneath all of the others. This new 2-dimensional representation of a football clearly shows which faces touch each other, making the colouring problem significantly easier to tackle. It is easy enough to show that three colours are not sufficient so all they need to do is to colour the diagram with four colours so that no two adjacent shapes are the same colour and the outer hexagons are coloured using only three colours (so that the hidden pentagon can be coloured in the fourth colour). This is a simple exercise that they will have no problems with. It can then be extended to a 3-edge-colouring problem, which is even more interesting!
That’s why I keep asking for these kinds of books. They give me so much inspiration and help me to steer clear of hum drum textbook learning once in a while. I know it’s a niche market but while they keep publishing this kind of material I will keep buying it. Sorry David, my quirky library is ever expanding.

No comments:
Post a Comment